Mini-batch gradient descent
배치 Batch
배치의 사전적 의미는 (일괄적으로 처리되는)집단이다. 배치는 한번에 여러개의 데이터를 묶어서 입력하는 것인데, GPU 의 병렬 연산 기능을 최대한 효율적으로 사용하기 위해 쓰는 방법이다.(GPU 의 병렬연산에 대한 설명 링크)
배치는 Iteration 1회당 사용되는 training data set 의 묶음이며, Iteration 은 정해진 batch size 를 사용하여 학습(forward - backward) 를 반복하는 횟수를 말한다.
Batch gradient descent(BGD)
전체 데이터 셋에 대한 에러를 구한 뒤 기울기를 한번만 계산하여 모델의 parameter 를 업데이트 하는 방법.
이름에 들어가는 Batch 때문에 혼동스러울 수도 있다.(Ian Goodfellow 또한 자신의 책에서 그렇게 말한다.) 여기서 말하는 batch 는 말 그대로 total training dataset 을 의미한다. 데이터를 분할해서 다룰 때 사용하는 'batch' 라는 단어는 엄밀히 'mini-batch'를 의미하지면 편의상 batch 와 혼용해서 사용하는 것.
처음엔 '한 개의 데이터마다 한 개의 기울기를 구할 수 있는데, 어떻게 전체 데이터 셋에 대해서 기울기를 한번만 구한다는 것인가?' 라는 의문을 가지며 BGD를 잘못 이해하고 있었다.
Gradient descent 라는 알고리즘 자체는 loss function 을 입력 데이터 x 에 대해 편미분해서 기울기를 계산하는 것이 아닌, 가중치 w 에 대해서 편미분을 하는 것이기 때문에, 기울기를 계산하는 것 자체는 입력 데이터 x 의 갯수와 상관이 없다.
에러값을 전체 데이터에 대한 loss function 의 합으로 정의하던 평균으로 정의하던 단순히 w 에 대한 편미분을 수행하면 되는 것.
BGD의 장점
● 전체 데이터에 대해 업데이트가 한번에 이루어지기 때문에 후술할 SGD 보다 업데이트 횟수가 적다. 따라서 전체적인 계산 횟수는 적다.
● 전체 데이터에 대해 error gradient 를 계산하기 때문에 optimal 로의 수렴이 안정적으로 진행된다.
● 병렬 처리에 유리하다.
BGD의 단점
● 한 스텝에 모든 학습 데이터 셋을 사용하므로 학습이 오래 걸린다.
● 전체 학습 데이터에 대한 error 를 모델의 업데이트가 이루어지기 전까지 축적해야 하므로 더 많은 메모리가 필요하다.
● local optimal 상태가 되면 빠져나오기 힘듦(SGD 에서 설명하겠음.)
Stochastic gradient descent(SGD)
추출된 데이터 한 개에 대해서 error gradient 를 계산하고, Gradient descent 알고리즘을 적용하는 방법.
모델의 레이어 층은 하나의 행렬곱으로 생각할 수 있고, 여러개의 묶음 데이터는 행렬이라고 생각 할 수 있다.
즉, 여러개의 묶음 데이터를 특정 레이어 층에 입력하는 것은 행렬 x 행렬로 이해할 수 있는데,
SGD는 입력 데이터 한 개만을 사용하기 때문에 한 개의 데이터를 '벡터' 로 표현하여 특정 레이어 층에 입력하는 것으로 이해할 수 있고 이는 벡터 x 행렬 연산이 된다.
SGD의 장점
● 위 그림에서 보이듯이 Shooting 이 일어나기 때문에 local optimal 에 빠질 리스크가 적다.
● step 에 걸리는 시간이 짧기 때문에 수렴속도가 상대적으로 빠르다.
SGD의 단점
● global optimal 을 찾지 못 할 가능성이 있다.
● 데이터를 한개씩 처리하기 때문에 GPU의 성능을 전부 활용할 수 없다.
Mini-batch gradient descent(MSGD)
엄밀히 따지면 MSGD 와 SGD 는 다른 알고리즘이지만 요즘엔 MSGD를 그냥 SGD라고 많이들 혼용해서 부른다. 그래서 Ian Goodfellow 책에서도 아래 그림처럼 MSGD 알고리즘을 설명할 때 SGD 라고 표현하고 있다.
출처: Deep Learning, Ian Goodfellow, Chap 8. 291pp.
위 알고리즘을 그림으로 간단하게 풀어서 설명하면 아래와 같다.
간단하게 그리다 보니 그림에 도형 갯수는 정확하지 않다. 어쨌든 전체 데이터셋에서 뽑은 Mini-batch 안의 데이터 m 개에 대해서 각 데이터에 대한 기울기를 m 개 구한 뒤, 그것의 평균 기울기를 통해 모델을 업데이트 하는 방법이다.
다시 간단하게 요약하면, BGD 와 SGD 의 장점만 빼먹고 싶은 알고리즘. 전체 데이터 셋을 여러개의 mini-batch 로 나누어, 한 개의 mini-batch 마다 기울기를 구하고 모델을 업데이트 하는 것.
예를들어, 전체 데이터가 1000개인데 batch size 를 10으로 하면 100개의 mini-batch 가 생성되는 것으로, 이 경우 100 iteration 동안 모델이 업데이트 되며 1 epoch 이 끝난다.
MSGD의 장점
● BGD보다 local optimal 에 빠질 리스크가 적다.
● SGD보다 병렬처리에 유리하다.
● 전체 학습데이터가 아닌 일부분의 학습데이터만 사용하기 때문에 메모리 사용이 BGD 보다 적다.
MSGD의 단점
● batch size(mini-batch size) 를 설정해야 한다.
● 에러에 대한 정보를 mini-batch 크기 만큼 축적해서 계산해야 하기 때문에 SGD 보다 메모리 사용이 높다.
batch size 또한 hyper parameter 로써 사용자가 직접 설정해야 하는 값이다. batch size 는 보통 2의 제곱수를 이용하는데, 많은 벡터 계산이 2의 제곱수가 입력될 때 빠르기 때문이다.
출처: https://light-tree.tistory.com/133 [All about:티스토리]
지수 가중 이동평균(Exponentially Weighted Averages)
지수 가중 이동평균은 경사하강법 및 미니배치 경사하강법보다 효율적인 알고리즘을 이해하기위해 알아야하는 개념입니다. 이 개념은 최근 데이터에 더 많은 영향을 받는 데이터들의 평균 흐름을 계산하기 위한 것으로 최근 데이터에 더 높은 가중치를 줍니다. 수식으로 알아보겠습니다.

여기서 vt는 t번째 데이터의 가중 지수가중이동평균입니다. 그리고 β 값은 하이퍼파라미터로 최적의 값을 찾아야하는데 보통은 0.9를 많이 사용합니다. 마지막으로 θt 는 t번째 데이터의 값입니다. 그럼 먼저 β 값을 변경해보면서 이 수식에 대한 이해를 해보겠습니다.
우선, β 가 0.9일 경우를 보겠습니다. 사실 이 때의 vt 는 이전 10개의 데이터의 평균과 거의 같습니다. 이는 아래 식으로 계산해낼 수 있습니다.

우선 지금은 β 에 따른 지수가중이동평균값을 이해하기위해 위 식이 성립하는 이유는 나중에 언급하겠습니다. 다시 돌아와서 β 가 0.9일때 지수가중이동평균 그래프는 다음과 같이 그려집니다. 아래 붉은선 그래프는 일년동안의 기온변화를 지수가중이동평균으로 나타낸 그래프입니다.
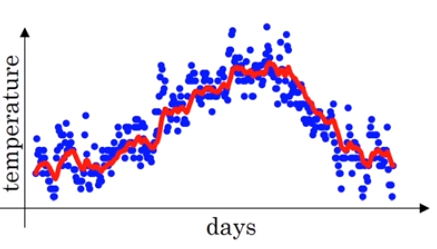
그렇다면 ββ 값을 조금 높여서 0.98일때는 어떤 그래프가 그려질까요?
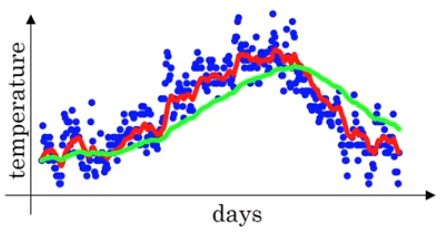
위와 같이 β가 0.98일때, 0.9일때보다 완만하고 부드러운 곡선인 이유는 1/(1-0.98)의 값이 50이므로 위 녹색 그래프는 50개 데이터의 평균값으로 만들어지기 때문입니다. 더 많은 데이터의 평균값을 이용하기 때문에 곡선이 더 부드러워 집니다. 이는 원래의 데이터의 값과 더 멀어진다고도 할 수 있습니다. 더 큰 범위 데이터에서 평균 낸 값이기 때문입니다. 여기서 내릴 수 있는 결론은 β 값이 클수록 선이 더 부드러워진다는 것입니다. 그렇다면 β 를 0.5로 낮춘다면 어떤 그래프가 그려질까요? 그래프를 그리기 이전에 어떻게 그려질지 예측할 수 있을 것입니다.
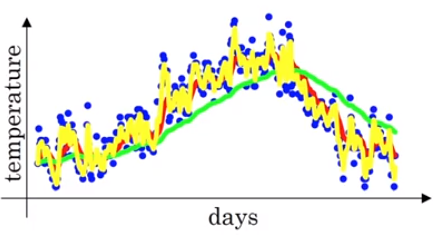
1/(1-0.5)의 값이 2이므로 2개의 데이터의 평균값으로 그래프가 그려집니다. 오직 2개의 데이터만 이용하므로 노이즈가 심하고 민감한 그래프가 그려지는 것입니다.
그럼 이제 처음에 봤던 지수가중이동평균 식을 상세하게 분석해 보겠습니다.
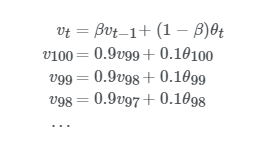
설명을 편하게 하기위해서 vtvt의 순서를 역순으로 했습니다. 맨 위에 v100v100 에 대한 식은 v99v99를 대체해주므로써 아래와 같이 표현할 수 있습니다.

그리고 위 식의 v98v98 을 또 다음과 같이 대체할 수 있습니다.
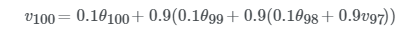
반복적으로 v 값을 대체해준 후 풀어쓰면 아래와 같은 식이 나오지요.

마지막 식을 통해서 규칙성을 파악하셨겠지만 vt 는 이전 데이터에 지수적으로 감소하는 함수를 곱해주고 모두 더해주는 것입니다. θ 앞의 계수들을 모두 더하면 1 또는 1에 가까운 값이 됩니다. 이는 아래서 자세히 설명드릴 편향보정 이라고 불리는 값 입니다. 이 값들에 의해 지수가중평균이 되는 것입니다. 그럼 vt 가 얼마나 많은 데이터의 평균값이 되는지 궁금하실 겁니다. 위 예시에서 사용한 β 값인 0.9의 10거듭제곱 값은 대략적으로 0.35와 같습니다. 이는 1e 값과도 대략적으로 같습니다. 일반적으로 표현하자면
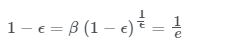
즉, 1e값이 되기까지 이전 10개의 데이터가 필요한 것입니다. 이를 한 눈에 이해하기 위해서 아래 그림을 확인해 보겠습니다.
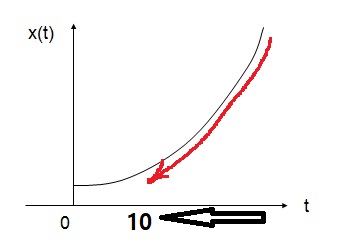
위 그림과 같이 10개 이전의 데이터의 가중치가 현재 가중치의 약 1/3로 줄어드는 것입니다. 이전에 예시로 들었던 ββ 값인 0.98의 경우 0.98^50이 대략적으로 1e 와 같습니다. 이는 이전에 언급했던 11−β11−β 를 관습적으로 쓰는 이유입니다. 1/(1−0.98)=501/(1−0.98)=50 이기 때문이지요.
실제로 구현할 때는 v0,v1,v2,...v0,v1,v2,... 을 모두 변수화 하지 않습니다. 아래와 같이 vθ 값을 덮어씌워 줍니다. (vθ 로 표시한 이유는 θ 를 매개변수로 하는 지수가중이동평균을 계산한다는 것을 나타내기 위함입니다.)
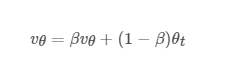
이렇게 vθ는 매번 업데이트 됩니다. 이렇게 지수평균값을 얻는 장점은 아주 적은 메모리를 사용한다는 점입니다. 가장 최근에 얻은 값을 계속 덮어쓰기만 하면 되니까요. 이 방법은 컴퓨터 계산비용과 메모리 효율 측면에서 더 효율적이기 때문에 오늘날 머신러닝에서 많이 사용하고 있습니다.
출처 : https://hansololee.github.io/optimization/exponentially_weighted_averages/
'Google ML Bootcamp' 카테고리의 다른 글
| [CNN]Deep Convolutional Models : Case Studies (0) | 2022.07.25 |
|---|---|
| [CNN] Foundations of Convolutional Neural Networks (0) | 2022.07.21 |
| Structuring Machine Learning Projects (0) | 2022.07.20 |
| practical aspects of deep learning (0) | 2022.07.11 |
| Logistic Regression as a Neural Network (0) | 2022.06.23 |



