[Train/Dev/Test Sets]
Training Set, Dev Set, Test Set을 잘 설정하면 좋은 성능을 갖는 NN을 빨리 찾는데 도움이 될 수 있다.
NN에서는 다음과 같이 결정해야 할 것들이 있다.
- # of layer
- # of hidden unit
- Learning Rate
- Activation Function
처음 새롭게 NN을 구현할 때에는 적절한 하이퍼 파라미터 값들을 바로 선택하기는 거의 불가능하다. 그래서, 반복적인 과정을 통해 실험하면서 하이퍼 파라미터 값들을 바꿔가며 더 좋은 성능을 갖는 NN을 찾아야 한다.

Applied ML is a highly iteration process
경험이 많은 딥러닝 개발자들도 적절한 파라미터를 한 번에 선택하는 것은 거의 불가능하다. 그래서 오늘날 적용된 딥러닝은 반복적인 과정을 통해서 실험하면서 더 좋은 신경망을 찾아간다. 여기서 중요한 것은 우리가 이 반복적인 과정을 얼마나 효율적으로 하느냐이다.
여기서 우리는 데이터를 Train/Dev/Test Set를 적절하게 설정하면 훨씬 효율적으로 수행할 수 있다.
[Bias / Variance]

Bias
- Bias(편향)는 예측값과 실제값의 차이이다.
- 즉, Bias(편향)가 크다는 것은, 예측값과 실제값의 차이가 크다는 것이며, 이는 과소적합을 의미한다.
Variance
- Variance(분산)는 입력에 따른 예측값의 변동성을 의미한다.
- 즉, Variance(분산)가 크다는 것은, 입력에 따른 예측값의 변동성이 크다는 것이며, 이는 과대적합을 의미한다.
Trade-off
- Trade-off는 시소처럼 한쪽이 올라가면 한쪽이 내려가는 관계를 의미한다.
예제 1

- 파란 점이 예측값, 빨간 원이 실제값을 의미한다.
- Bias가 높다는 것은, 예측값과 실제값의 오차가 크다는 것을 의미한다. (과소적합 상황)
- Variance가 높다는 것은, 예측값의 변동성이 크다는 것을 의미한다. (과대적합 상황)
예제 2

- 왼쪽 그래프는 큰 bias, 작은 variance
- 오른쪽 그래프는 작은 bias, 큰 variance
- 왼쪽 그래프의 예측 값, 실제 값이 차이는 오른쪽 그래프보다 크다. (큰 bias)
- 오른쪽 그래프의 예측 값, 실제 값의 차이는 0이다. (작은 bias)
- 왼쪽 그래프는 일반화가 잘 되어 있기 때문에 예측 값이 일정한 패턴을 나타낸다. (작은 variance)
- 오른쪽 그래프는 예측 값이 일정한 패턴 없이 들쑥날쑥하다. (큰 variance)
예제 3

- 모델을 학습을 시킬수록 모델의 복잡도는 더 올라간다.
- 이를 X축 모델 복잡도(model complexity)로 표현하면,
- 모델이 단순해질수록, Bias는 증가하고 Variance는 감소한다. (과소적합 상황)
- 모델이 복잡해질수록, Bias는 감소하고 Variance는 증가한다. (과대적합 상황)
- 결국, 전체 Error는 Bias와 Variance 간의 Trade-off 관계 때문에, 계속 학습 시킨다고 해도 쉽게 줄어든지 않는다.
- 즉, 무조건 Bias만 줄일 수도, 무조건 Variance만 줄일 수도 없기 때문에, Bias와 Variance의 합이 최소가 되는 적당한 지점을 찾아 최적의 모델을 만들어야한다.
[Regularization]
- 먼저 L1 Regularization 과 L2 Regularization 을 설명
- 결론부터 얘기하자면 L1 Regularization 과 L2 Regularization 모두 Overfitting(과적합) 을 막기 위해 사용됩니다.
- 위 두 개념을 이해하기 위해 필요한 개념들부터 먼저 설명하겠습니다.
- 글의 순서는 아래와 같습니다.
- Norm
- L1 Norm
- L2 Norm
- L1 Norm 과 L2 Norm 의 차이
- L1 Loss
- L2 Loss
- L1 Loss, L2 Loss 의 차이
- Regularization
- L1 Regularization
- L2 Regularization
- L1 Regularization, L2 Regularization 의 차이와 선택 기준
Norm

- Norm 은 벡터의 크기를 측정하는 방법입니다.
- 두 벡터 사이의 거리를 측정하는 방법이기도 합니다.
- 여기서 p 는 Norm 의 차수를 의미합니다.
- p = 1 이면 L1 Norm 이고, P = 2 이면 L2 Norm 입니다.
- n은 해당 벡터의 원소 수 입니다.
L1 Norm

- L1 Norm 은 벡터 p, q 의 각 원소들의 차이의 절대값의 합입니다.
- 예를 들어, 두 벡터 p =(3, 1, -3), q = (5, 0, 7) 의 L1 Norm을 구한다면
- |3-5| + |1-0| + |-3 -7| = 2 + 1 + 10 = 13 이 됩니다.
L2 Norm

- L2 Norm 은 벡터 p, q 의 유클리디안 거리(직선 거리) 입니다.
- 여기서 q 가 원점이라면, 벡터 p, q의 L2 Norm 은 벡터 p와 원점 간의 직선거리라고 할 수 있습니다.
- 예를 들어, 두 벡터 p =(3, 1, -3), q = (0, 0, 0) 의 L2 Norm 을 구한다면
- 3^2 + 1^2 + (-3)^2 = 19 가 됩니다.
L1 Norm과 L2 Norm 의 차이

- 검정색 두 점사이의 L1 Norm 은 빨간색, 파란색, 노란색 선으로 표현 될 수 있고
- L2 Norm 은 오직 초록색 선으로만 표현될 수 있습니다.
- L1 Norm 은 여러가지 path 를 가지지만 L2 Norm 은 Unique shortest path 를 가집니다.
- 예를 들어 p = (1, 0), q = (0, 0) 일 때 L1 Norm = 1, L2 Norm = 1 로 값은 같지만 여전히 Unique shortest path 라고 할 수 있습니다.
L1 Loss
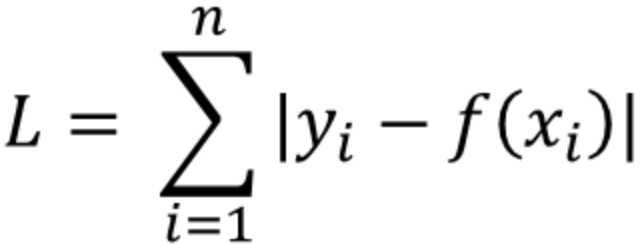
- y_i 는 실제값을, f(x_i)는 예측값을 의미합니다.
- 실제값과 예측값 사이의 오차의 절대값을 구하고, 그 오차들의 합을 L1 Loss 라고 합니다.
- 이를 Least absolute deviations(LAD), Least absolute Errors(LAE), Least absolute value(LAV), Least absolute residual(LAR), Sum of absolute deviations 라고 부릅니다.
L2 Loss

- L2 Loss 는 오차의 제곱의 합으로 정의됩니다.
- 이를 Least squares error(LSE) 라고 부릅니다.
L1 Loss, L2 Loss 의 차이
- L2 Loss 는 직관적으로 오차의 제곱을 더하기 때문에 Outlier 에 더 큰 영향을 받습니다.
- "L1 Loss 가 L2 Loss 에 비해 Outlier 에 대하여 더 Robust(덜 민감 혹은 둔감) 하다." 라고 표현 할 수 있습니다.
- Outlier 가 적당히 무시되길 원한다면 L1 Loss 를 사용하고
- Outlier 의 등장에 신경써야 하는 경우라면 L2 Loss 를 사용하는 것이 좋겠습니다.
- L1 Loss 는 0인 지점에서 미분이 불가능하다는 단점 또한 가지고 있습니다.
Regularization
- 보통 번역은 '정규화' 라고 하지만 '일반화' 라고 하는 것이 이해에는 더 도움이 될 수도 있습니다.
- 모델 복잡도에 대한 패널티로, 정규화는 Overfitting 을 예방하고 Generalization(일반화) 성능을 높이는데 도움을 줍니다.
- Regularization 방법으로는 L1 Regularization, L2 Regularization, Dropout, Early stopping 등이 있습니다.
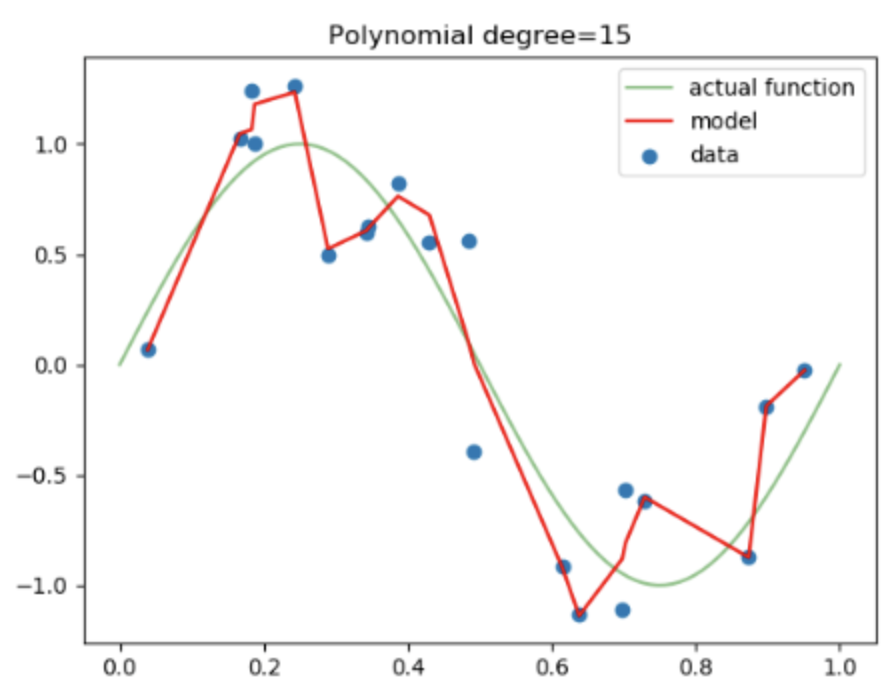
- model 을 쉽게 만드는 방법은 단순하게 cost function 값이 작아지는 방향으로 진행하는 것입니다.
- 하지만, 이럴 경우 특정 가중치가 너무 큰 값을 가지게 될수도 있습니다.
- 가중치가 큰 값을 가진다는 것은 모델의 일반화 성능이 떨어진다는 것을 의미합니다. (과대적합)
- 위 그래프에서 actual function 이 target function 이라고 했을 때, model 이 데이터에 overfitting 된 것을 알 수 있습니다.

- 따라서, 위 그래프처럼 모델에 Regularization 을 적용한다면, 특정 가중치가 너무 과도하게 커지지 않게 됩니다.
L1 Regularization
- L1 Regularization을 사용해 새롭게 정의된 cost function

- 논문에 따라서 가중치의 절대값 앞에 분수로 붙는 1/n 이나 1/2 가 달라지는 경우가 있는데
- L1 Regularization 의 개념에서 가장 중요한 것은 cost function 에 가중치의 절대값을 더해준다는 것이기 때문에
- 1/n 이나 1/2 가 달라지는 경우는 연구의 case 에 따라 다르다고 이해하고 넘어가겠습니다. (이는 L2 Regularization 또한 같습니다).
- 기존의 cost function 에 가중치(W)의 크기가 포함되면서,
- 학습의 방향이 단순하게 cost function의 값이 작아지는 방향으로만 진행되는 것이 아니라,
- 가중치(W) 또한 작아지는 방향으로 학습이 진행됩니다.
- 이때 λ 는 상수로 0에 가까울 수록 정규화의 효과는 없어집니다.
- 새롭게 정의된 cost function을 w에 대해 편미분한 결과

- w의 크기와 상관없이 w의 부호에 따라 상수값을 빼주는 방식
- L1 Regularization 을 사용하는 Regression model 을 Least Absolute Shrinkage and Selection Operater(Lasso) Regression 이라고 부릅니다.
L2 Regularization
- L2 Regularization을 사용해 새롭게 정의된 cost function

- 기존의 cost function 에 가중치의 제곱을 더함으로써
- L1 Regularization 과 마찬가지로 가중치가 너무 크지 않은 방향으로 학습되게 됩니다.
- 새롭게 정의된 cost function을 w에 대해 편미분한 결과
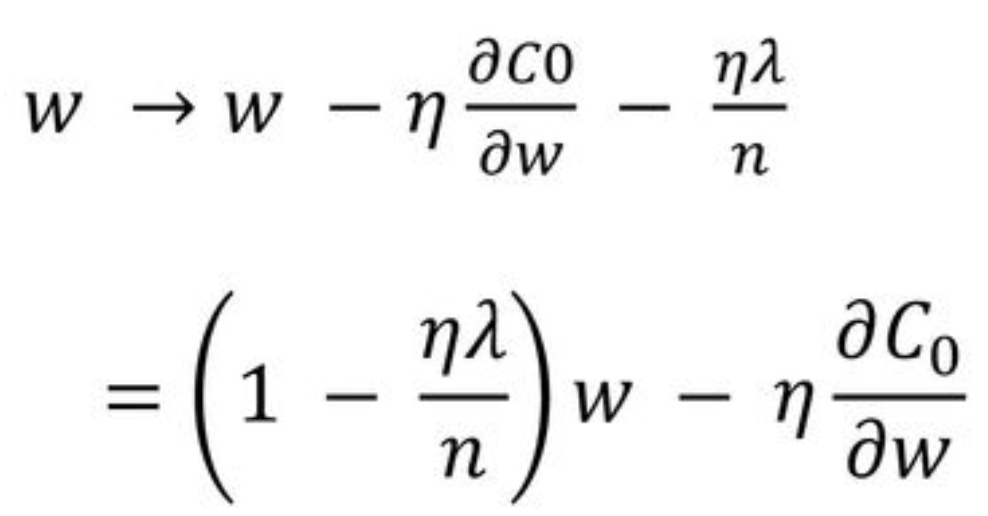
- w 에 ( 1-nλ/n ) 을 곱함으로써 w 값이 작아지는 방향으로 진행
- 이를 Weight decay라고 함
- L2 Regularization 을 사용하는 Regression model 을 Ridge Regression 이라고 부릅니다.
L1 Regularization, L2 Regularization 의 차이와 선택 기준
- L1 Regularization은 가중치 업데이트 시, 가중치의 크기에 상관 없이 상수값을 빼면서 진행됩니다.
- 때문에 작은 가중치들은 거의 0으로 수렴 되어, 몇개의 중요한 가중치들만 남게 됩니다.
- 그러므로 몇 개의 의미 있는 값을 끄집어내고 싶은 sparse model 같은 경우에는 L1 Regularization이 효과적입니다.
- 다만, L1 Regularization은 아래 그림처럼 미분 불가능한 점이 있기 때문에 Gradient-base learning 에는 주의가 필요합니다.

- L2 Regularization은 가중치 업데이트 시, 가중치의 크기가 직접적인 영향을 미칩니다.
- 따라서, L2는 L1 보다 가중치 규제에 좀 더 효과적입니다.
[Gradient Checking]

- Gradinet checking은 Forward propagation, Backward propagation 이후, backward propagation으로 구해진 역전파값이 정확한지 점검하는 과정이다.
- 학습 단계에서 사용하는 것이 아니라 디버깅 단계에서 사용한다. 왜냐하면, 한 번 학습할 때마다 Gradient checking할 경우 시간이 너무 오래 소요되기 때문이다.
- 수식으로 정의된 Derivative(혹은 Gradient)값과 Backward progation으로 구해진 값이 동일하거나 근소한 차이를 보이는지 확인한다.
- 구체적으로, delta에 속하는 여러가지 파라미터들(W,b...)들을 각 레이어에 속한 각 뉴런값들을 n by 1차원의 메트릭스로 표현한다. (n=전체 모델이 학습시켜야 하는 파라미터의 총 개수)
- 여러 파라미터의 각 값의 grad, gradapprox, grad-gradapprox의 노름값을 numpy의 np.linalg.norm함수를 사용하여 구한다.
- 만약, gradient checking시 문제가 생겼다면, 순차적으로 레이어를 훑으면서 어느 값이 잘못되었는 찾아본다.
- Regularization을 적용하였을 때, 이 부분을 반영하여 gradient checking해야 한다.
- Drop-out을 적용하여 학습했을 때에는 Gradient checking을 실행할 수 없다. Dropout을 끈 상태에서 Gradient checking을 먼저 해보고, 이상이 없다면 drop-out시에도 이상이 없는 것으로 편의상 간주한다.
'Google ML Bootcamp' 카테고리의 다른 글
| [CNN]Deep Convolutional Models : Case Studies (0) | 2022.07.25 |
|---|---|
| [CNN] Foundations of Convolutional Neural Networks (0) | 2022.07.21 |
| Structuring Machine Learning Projects (0) | 2022.07.20 |
| Optimization Algorithms (0) | 2022.07.13 |
| Logistic Regression as a Neural Network (0) | 2022.06.23 |